
Imagine a chill Monday morning after a relaxing weekend, while going to work, you enter an empty elevator. Your destination is the 11th floor. Just before the door closes, a guy hastily enters. After a brief greeting, he impatiently presses the button for the 3rd floor a few times. The elevator soon moves to this floor and he enters his office. It then continues upwards to the next intended floor. Notice that despite that person pressing the elevator button multiple times, it only stopped once at the intended destination. Why do you think this happens? Is it by design or by default? Welcome to idempotency in action!
1. Hello Idempotency.
Idempotency is defined as the property of an operation that can be performed multiple times without changing some final results or having any side effects.
The term was coined by mathematical philosopher Benjamin Peirce in his self-published 1870 book - Linear Associative Algebra.
According to him, idempotency means the quality of having the same power.
Idempotency is essential not only in mathematics and computer science but also from a philosophical perspective that affects our day-to-day life.
2. Idempotency In Philosophy.
When you hear philosophy, you might think of an ancient Greek arena with Socrates, Plato and Aristotle debating about this magical term. Interestingly, idempotency is present in philosophy more than you can imagine.
First, let’s remind ourselves, what is philosophy?
Philosophy (love of wisdom in ancient Greek) is a systematic study of general and fundamental questions concerning topics like existence, reason, knowledge, values, mind, and language. It is a rational and critical inquiry that reflects on its own methods and assumptions.
In other words, philosophy is like a treasure hunt for answers to big questions about life, the universe, and everything in between. It's a way of thinking and exploring that helps us understand the world around us and how we fit into it.
In philosophy, idempotency can be seen as a principle of non-interference. It means that an action should not have any unintended consequences, even if it is performed multiple times. This is important in many areas of philosophy, such as ethics, politics, and law.
Let’s consider an example of ethics, which is the study of what’s right and wrong. Here, idempotency is seen as a means of understanding repeated actions that do not increase or decrease their harm/goodness on each repetition. In particular, we can think of an idempotent ethical action as one that does not cause more harm or good even if it’s performed multiple times.
In law, the role of an idempotent action is a way of ensuring fairness without disadvantaging anyone even if that action is performed multiple times. For example, many legal systems guard against double jeopardy, which prevents someone from being tried for the same crime twice.
Furthermore, when we talk about philosophy, we also think about logic, which is highly relevant to idempotency. In logic, an operation is idempotent if applying it on the same value results in that value itself. So, applying it multiple times, on a particular value, doesn't change the result after the first application.
For example, let's illustrate the idempotent property of the logical AND operation (⋀) using a truth table:
| A | B | A ⋀ B | (A ⋀ B) ⋀ (A ⋀ B) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
In this truth table, we have two propositions (A and B) and we're evaluating the logical AND operation between them (denoted as A ⋀ B). The third column represents the result of the initial AND operation.
The fourth column represents the result of applying the AND operation (A ⋀ B) again to its own result (A ⋀ B). As you can see, the values in the third and fourth columns are the same for all combinations of A, B and A ⋀ B. Crucially, applying the AND operator on any truth value with itself results into that value itself.
Fun Trivia.
- Click on any article on Wikipedia.
- Click on the first non-parenthesized, non-italicized link.
- Ignore external links.
- You will eventually reach the Wikipedia article about “Philosophy”.
- Fun exercise: try to automate steps 1 to 4.
3. Idempotency In Maths.
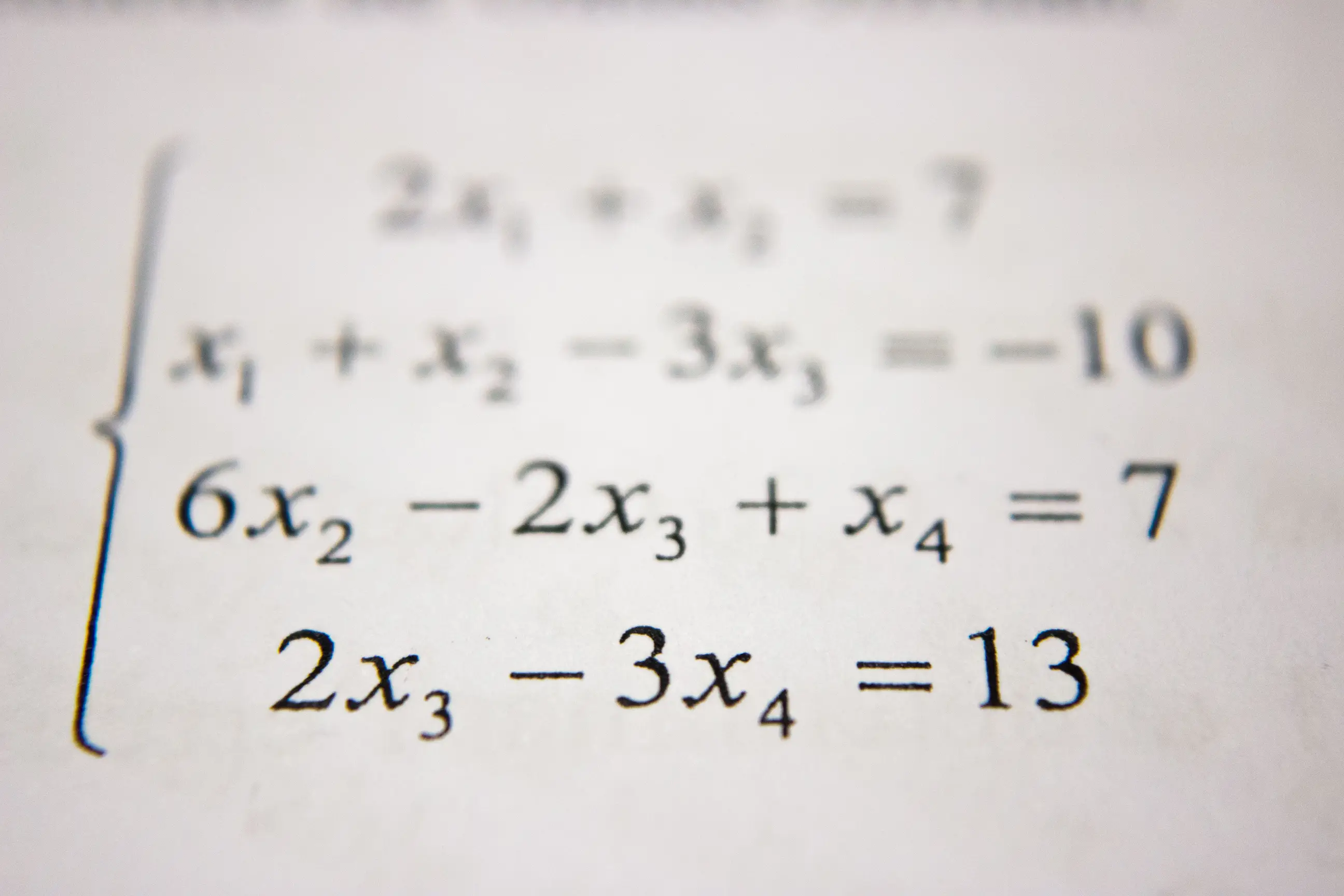
During his logical, mathematical and research work, Benjamin Peirce noticed there were special numbers that didn’t change no matter how many times you applied an operation to them. Let’s take a look at them.
Firstly, adding zero to any number, even when performed multiple times won’t change the outcome.
Secondly, multiplying any number by 0 results in 0.
Thirdly, raising 0 to any power, like 0^2, always results in 0.
Fourth, 1 raised to any power, like 1^2, always results in 1.
Let’s now look at a unary operation on a number that’s idempotent.
Consider the absolute value function, denoted as |x|, which gives the distance of a number from zero. For real numbers, applying the absolute value function twice doesn't change the result beyond the first application:
||x|| = |x|
Here’s an example with Ruby:
n = -7
n.abs # => 7
(n.abs).abs # => 7
((n.abs).abs).abs # => 7
4. Idempotency In Day-To-Day Life.
Prof. Richard Feynman, a Nobel Prize-winning physicist, strongly believed in learning via examples. For him, the best way to learn a new concept was to see it in action and understand how it interacted with real life.
Allow me therefore to share examples of how idempotency affects our daily lives.
Several years ago, some friends and cousins sat down on a cosy sofa to play fighting games. After the initial screen loaded, the text “press any button to continue” appeared. At this point, those with controllers literally started smashing all the buttons so that the game started faster.
We’ve all done that.
The reality is, once a button was pressed, the game was going to load another state and the remaining presses — despite how enthusiastic we were — wouldn’t change a thing. We can picture that button as the following automaton state. Once we leave that state, we do not get back to it.
I introduced this article with an example of an elevator but this also applies to crosswalk buttons. Often, we see several people impatiently pressing the buttons. Yet, the state doesn’t change any faster and the outcome is the same as if it were pressed the first time.
5. Idempotency In Computer Science.
As a software engineer, you might have heard of pretty printing. This operation is idempotent - if the output is already pretty, pretty-printer does nothing. The same goes for code formatters like JSON viewer. If your JSON document is already well-formatted, it will stay the same the second time.
Here’s a code in Ruby IRB for illustration:
require 'httparty'
url = 'https://jsonplaceholder.typicode.com/todos/1'
response = HTTParty.get(url)
print = pp r
=> {"userId"=>1, "id"=>1, "title"=>"delectus aut autem", "completed"=>false}
pp print
=> {"userId"=>1, "id"=>1, "title"=>"delectus aut autem", "completed"=>false}
Generally, in computer science, idempotency refers to a property of certain operations or functions that, when applied multiple times, produce the same result as if they were applied once or a single time. This concept is particularly relevant in distributed systems, network protocols, test automation and APIs, where ensuring consistent and predictable outcomes is crucial.
Let’s look at a simple example using the Set data structure.
require 'set'
# Create a set of unique numbers
numbers_set = Set.new([1, 2, 3, 4])
# Display the set before adding an existing number
puts "Numbers set before adding: #{numbers_set}"
# Output: Numbers set before adding: #<Set: {1, 2, 3, 4}>
# Add an existing number to the set twice
numbers_set.add(3)
numbers_set.add(3)
# Display the set after adding an existing number
puts "Numbers set after adding: #{numbers_set}"
# Output: Numbers set after adding: #<Set: {1, 2, 3, 4}>
If we add an existing value to a set, nothing changes.
6. REST API
Some Restful APIs are designed to be idempotent with requests such as GET, HEAD, OPTIONS and TRACE. They don’t change the data.
GET /api/users/12345
This GET request does not alter the server's state, and even if executed repeatedly, the user data will be returned consistently.
PUT & DELETE despite changing the data does so only once i.e. if you delete a resource once or many times, the resource is deleted only once. Same with PUT which is an update operation.
Consider an example using HTTParty in Ruby:
require 'httparty'
url = 'https://api.example.com/api/users/12345'
response = HTTParty.delete(url)
if response.success?
puts 'User deleted successfully'
else
puts 'Error deleting user'
end
7. Functional Programming.
When we talk about functional programming, we mostly talk about two types of functions:
- without side effects.
- with side effects.
For functions without side effects, idempotency means that no additional side effects are caused after the first application.
A simple example of the first case:
def factorial(n)
if n == 0
return 1
else
return n * factorial(n - 1)
end
end
factorial(5) # => 120
factorial(5) # => 120
This function is pure because it doesn’t modify any state outside of its own scope and calling it multiple times with the same input returns the same output.
An example of a function with side effects:
def log_message(message)
# Only log the message once.
if !@logged_message
@logged_message = true
logger.info(message)
end
end
log_message('Hello, world!') # => 'Hello, world!'
log_message('Goodbye, world!') # => 'Goodbye, world!'
log_message('Hello, world!') # =>
This function takes a message as input and logs the message to the console. The function does not modify any state outside of its own scope. However, it does have a side effect: it logs the message to the console.
The @logged_message variable is used to track whether the message has already been logged. The first time the function is called, the value of @logged_message is false. The function then sets the value of @logged_message to true and logs the message to the console. The next time the function is called, the value of @logged_message is still true, so the function does not log the message again.
Idempotency is a phenomenon that’s reflected everywhere in our daily lives similar to the Golden Ratio. Each time you turn on a switch, that’s idempotency in action. In this post, we’ve seen how it applies to Philosophy and is an important discussion in the design of Computer Systems. From Distributed Architecture, Test Automation, and Payment Gateways to building resilient and efficient systems, idempotency is incredibly relevant.
PS.
- Philosophy (Wikipedia - 2023, August 3).
- Idempotent Operations.
- Prettyprint (Wikipedia - 2023, June 1).
- Aristotle - Nicomachean Ethics. Translated by W.D. Ross. Oxford: Oxford University Press, 1925.
- What Is Idempotence?.
- Idempotence (Wikipedia - 2023, July 22).